Recordando la parte uno...
Las condiciones iniciales que nos ayudaron a encontrar el periódo, se establecieron de una manera muy intuitiva, una manera más formal sería que:
Donde 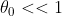 es el ángulo que se levanta inicialmente el péndulo. Estas condiciones son, que al momento de iniciar el reloj tengamos el pendulito levantado, y que esté en un máximo. Establecido esto, podemos determinar que
es el ángulo que se levanta inicialmente el péndulo. Estas condiciones son, que al momento de iniciar el reloj tengamos el pendulito levantado, y que esté en un máximo. Establecido esto, podemos determinar que 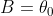 . Como dijimos anteriormente, esto sólo funciona cuando ese ángulo es pequeño, ahora veremos como resolverlo para ángulos arbitrarios.
. Como dijimos anteriormente, esto sólo funciona cuando ese ángulo es pequeño, ahora veremos como resolverlo para ángulos arbitrarios.
Por simple conservación de energía, si el péndulo se encuentra suspendindo a una altura relativa h
tenemos que
Nota: Si derivamos una vez más, con respecto a t, obtenemos el mismo resultado del post anterior, pero sin usar el formalismo lagrangiano. También se puede obtener mediante análisis de fuerzas (tal vez lo haga como bonus en otro post).
Ahora viene la parte interesante, la parte que involucra ángulos arbitrarios. Comencemos dividiendo entre l, y después invirtiendo la última ecuación
Para obtener el periodo, necesitamos integrar sobre una vuelta completa:  , y de regreso. Por la simetría del problema, podemos también integrar dos veces, sobre media vuelta, o cuatro veces sobre un cuarto de vuelta. Entonces, obetenemos
, y de regreso. Por la simetría del problema, podemos también integrar dos veces, sobre media vuelta, o cuatro veces sobre un cuarto de vuelta. Entonces, obetenemos
La integral de la derecha no se puede resolver analíticamente (no me refiero a lo analítico de cálculo complejo, sino a que no puede ser expresada en términos de funciones elementales). Esta integral, sin embargo, es una función elíptica del tipo 1
) ,
,=%20\frac{\pi}{2}%20\sum_{n=0}^{\infty}%20\left[%20\left(%20\frac{(2n)!}{(2^n%20\cdot%20n!)^2}%20\right%20)^2%20{\rm%20sen}^{2n}\left(%20\frac{\theta_0}{2}%20\right)%20\right]) .
.^2%20{\rm%20sen}^2%20\left(%20\frac{\theta_0}{2}%20\right%20)%20+%20\left(%20\frac{1\cdot%203}{2\cdot%204}\right%20)^2%20{\rm%20sen}^4%20\left(%20\frac{\theta_0}{2}%20\right%20)+\cdots\right])
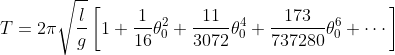
donde,
De esta manera,
Para vernos más domingueros más clara la contribución del ángulo inicial, hagamos la expansión en serie del Seno, y enchufémosla en la expresión anterior
Cuando el ángulo inicial es pequeño, hemos visto que el periodo no depende de dicho ángulo. Para ángulos arbitrarios vemos que sí. Puesto que no conozco exactamente cuanto es el ángulo inicial de cada oscilación del columpio de Heidi, aquí les dejo una gráfica de como cambia la longitud en función de tal ángulo (hasta orden de 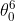 ).
).
Podemos notar que para ángulos pequeños, el resultado es prácticamente el mismo que en el post anterior. Hemos graficado hasta un ángulo de 90 grados (Pi/2).

No hay comentarios.:
Publicar un comentario
Write here a comment/Deja aquí un comentario